给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
复制
示例 2:

输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
复制
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
步骤1:题目分析
目标:在给定的 m 行 n 列矩阵 matrix 中,从左上角开始,按顺时针顺序遍历矩阵,返回所有元素的顺序列表。
输入输出条件:
- 输入矩阵
matrix的大小为m x n,即有m行和n列。 - 输出为按顺时针顺序排列的矩阵元素列表。
限制条件:
1 <= m, n <= 10,即矩阵最大为 10x10 的大小。- 每个矩阵元素的值在
-100 <= matrix[i][j] <= 100的范围内。
边界条件:
- 单行或单列矩阵(例如
1xN或Mx1)的特殊情况。 - 矩阵大小为
1x1的情况。 - 空矩阵(在此题中不会出现,因为
m和n均不小于 1)。
步骤2:解题思路与步骤分解
算法设计: 我们可以通过模拟顺时针遍历的方式来解决这个问题,即通过设定矩阵的四个边界(上、下、左、右)逐层向内收缩。这种方法是双指针法的变体。
解决方案步骤:
- 初始化边界:
- 定义四个变量表示矩阵的边界:
top为上边界,初始值为 0。bottom为下边界,初始值为m - 1。left为左边界,初始值为 0。right为右边界,初始值为n - 1。
- 定义四个变量表示矩阵的边界:
- 按顺时针方向遍历矩阵:
- 使用循环依次遍历矩阵的边界,依次向内缩小边界:
- 从左到右遍历上边界,将元素添加到结果列表中,
top向下移动(top++)。 - 从上到下遍历右边界,将元素添加到结果列表中,
right向左移动(right--)。 - 从右到左遍历下边界(如果下边界仍然在
top下方),bottom向上移动(bottom--)。 - 从下到上遍历左边界(如果左边界仍然在
right左方),left向右移动(left++)。
- 从左到右遍历上边界,将元素添加到结果列表中,
- 使用循环依次遍历矩阵的边界,依次向内缩小边界:
- 循环终止条件:
- 当
top超过bottom或left超过right时,所有元素都已访问完毕,退出循环。
- 当
时间复杂度和空间复杂度:
- 时间复杂度:O(m * n),因为每个元素都会被访问一次。
- 空间复杂度:O(1),如果不计输出所占的空间。
步骤3:C++ 实现代码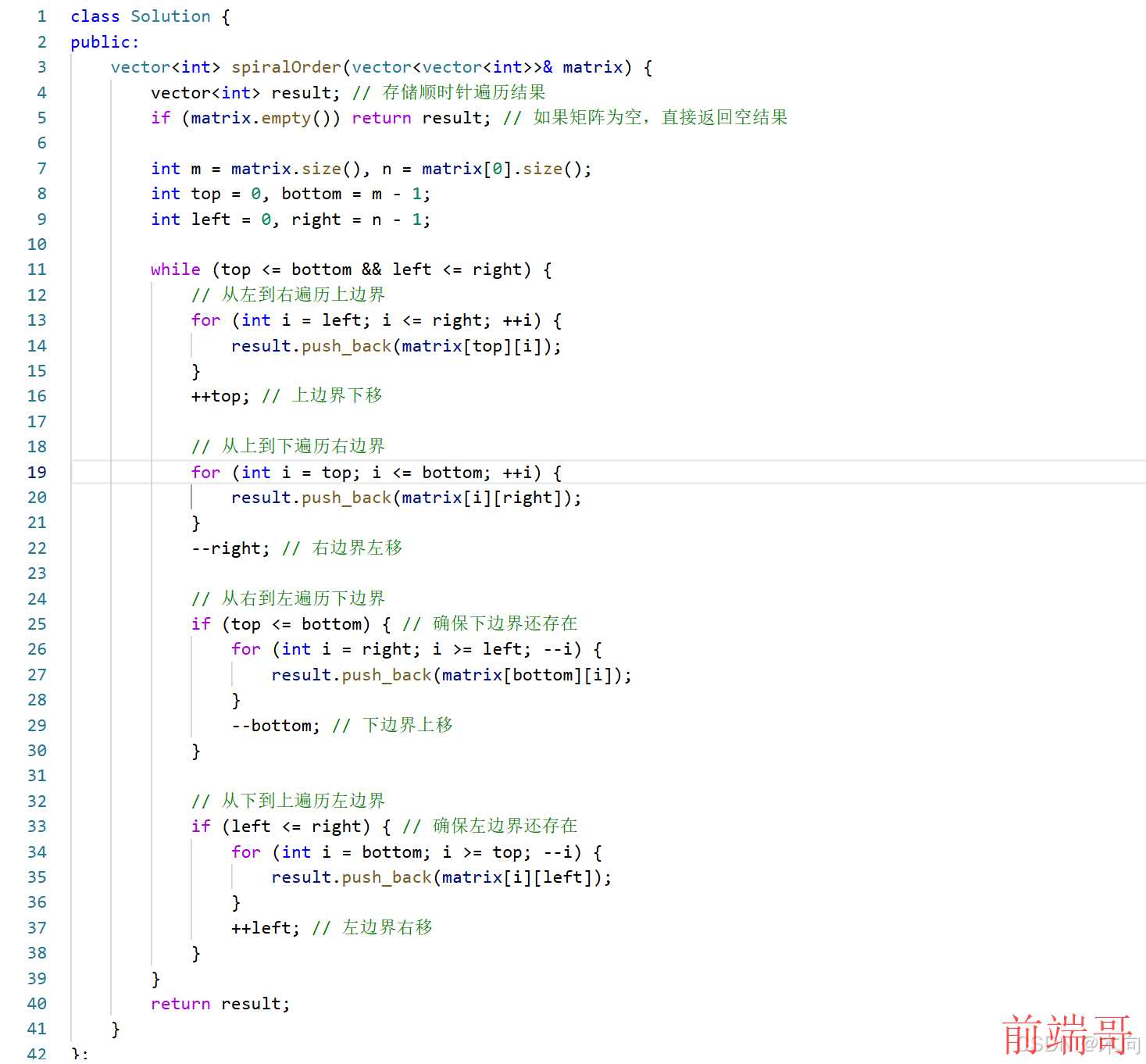
代码解释:
- 本代码使用一个
result向量存储遍历的结果。 - 按顺时针方向依次处理上、右、下、左边界,每遍历完一条边界就将对应边界缩小,确保按螺旋顺序。
- 使用条件判断确保边界仍然存在,避免重复访问。
步骤4:解题启发
此题体现了双指针法和边界控制在解决二维矩阵问题中的应用。通过限制边界逐步向内收缩,可以高效地完成矩阵遍历。此外,按螺旋顺序访问矩阵也可以应用到其他变形场景(如逆时针、反向等),增加了二维数据的遍历灵活性。这种方法能够减少不必要的重复访问,在数据量较大时可以保持较高的效率。
步骤5:实际应用场景
螺旋顺序遍历的算法可以在许多实际场景中使用,特别是在图像处理和硬件操作中,例如:
- 打印电路板(PCB)检测:在制造 PCB 时,需要对电路板上的焊点进行检查。使用螺旋遍历可以将检测头从中心开始逐层检测,以确保所有区域都能被遍历到。这种螺旋顺序可以减少检测器的移动次数,从而提升检测效率。
实现方式:
- 将 PCB 表面映射为二维矩阵,将检测点定义为矩阵的元素。
- 使用螺旋遍历算法控制检测头的移动路径,从中心开始螺旋式向外扩展。
- 每个点被访问时,检测设备执行一次焊点检测操作,记录检测结果。
此方法可以减少检测头的移动距离和时间,提高生产效率,并降低检测的整体能耗。

