说在开头:关于德布罗意的电子波(1)
德布罗意家族的历史悠久,他的祖先中出了许许多多将军、元帅、部长,参加过法国几乎所有的战争和各种革命,后来受到路易.腓力的册封,继承了这最高世袭身份的头衔:公爵。路易斯.德布罗意的哥哥:莫里斯.德布罗意便是第六代德布罗意公爵;当1960年莫里斯去世以后,路易斯终于从他哥哥那里继承了这个光荣称号:第七代德布罗意公爵。
路易斯.德布罗意从小对历史很感兴趣,他的哥哥莫里斯.德布罗意是一位著名的放射线物理学家,并在1911年参加了第一届索尔维会议,他将会议记录带回了家;小路易斯看到了这些激动人心的科学进展和最新思潮,完全被物理学给吸引了,于是他立志成为物理学家。德布罗意进入大学学习物理,导师是著名的保罗.郎之万,他一直在思考一个问题:如何能够在波尔的原子模型里面自然而然的引进一个周期的概念,以符合观测到的现实。原本这个条件是强加在电子上面的量子化模型:电子的轨道是不连续的。但是为什么必须如此呢?对于这个问题,玻尔做了硬性的规定,而没有解释原因,而电子只能听玻尔的话,乖乖的做着不连续的运动。德布罗意想,是时候释放你们的天性了,自由的飞翔吧。
1919 ~1922年,小布里渊发布了一系列关于玻尔原子的论文,试图解释只存在分离的定态轨道这一个事实,在老布里渊(小布里渊他爹)看来,那是因为电子在运动的时候会激发周围的“以太”(虽然爱因斯坦已经宣判了“以太”死刑,但是只有老一辈人的时代彻底结束,才能让“以太”真正死亡),这些被振荡的“以太”形成一种波动,它们相互干渉,在绝大部分地方抵消掉了,因此“以太”不能出现在那里。德布罗意看了布里渊的文章后就所有启发,虽然“以太”那玩意实在让人不爽。德布罗意又想到了爱因斯坦的相对论,他开始这样推论:根据爱因斯坦那个著名的方程,如果电子有质量m,那么它一定有一个内禀的能量:E = m*C²。我们再回顾下量子基本方程:E = h*v,也就是说对应这个能量,电子一定会具有一个内禀的频率。这个频率的计算也很简单: m* C²= E =h*v,所以v = m*C²/h。
那这个电子内禀的频率又是啥玩意呢?它是某种振动的周期,那么我们又得出结论:电子内部有某些东西在振动。那又是什么东西在振动呢?德布罗意借助相对论,开始了他的运算,结果发现当电子以速度v0前进时,必定伴随着一个速度为C²/ v0的波……,这个波的速度将比光速C还要快上很多,德布罗意又证明:这种波不能携带实际的能量和信息,因此不违反相对论。爱因斯坦只说了:没有一种能量信号的传递能超过光速;所以对于德布罗意波也就打了个马虎就应付过去了。德布罗意称这种波为“相波”,后人也称之为“德布罗意波”。 (参考自:曹天元-上帝掷骰子吗)
二,MOS管导通过程
1,MOS管特征曲线
在具体分析MOS管导通过程之前,我们首先需要了解下MOS管的特征曲线;如下图所示以N沟道增强型MOS管为例的V-I特征曲线,横轴为VDS电压,纵轴为ID电流。整个曲线图分为4部分:截止区,可变电阻区,恒流区,击穿区。

1. 截止区(夹断区):当满足VGS < VGS(th) ,MOS管进入截止区;截止区位于特征曲线下方,表示MOS管不能导通处于截止状态;
2. 恒流区(饱和区):当VGS > VGS(th),且VDS > VGS-VGS(th)时,MOS进入恒流区;
——恒流区在输出特性曲线中间的位置,电流ID基本不随VDS变化, ID的大小主要决定于电压VGS;当MOS用来做放大电路时就是工作在恒流区。
3. 可变电阻区:当满足VGS> VGS(th), 且VDS > VGS-VGS(th)时,MOS管进入可变电阻区;
——在可变电阻区,ID随着VDS的增加而上升,两者基本上是线性关系,另外VGS不同RDS的阻值也会不同,我们一般看到的MOS管Datasheet中RDS(ON)参数是可变电阻区的导通电阻值。
2,MOS管导通过程
通过之前章节的分析,我们知道打通MOS管,需要VGS达到一定的电压;如下左图所示,以增强型NMOS为例,假设驱动芯片通过串阻RGATE来驱动MOS管G极电压。如下为MOS管理想的导通过程分析:
1. t0->t1阶段:驱动通过RGATA对Ciss充电,电压VGS以指数的形式从0V上升至Vth;
1, 本阶段VGS<VGS(th),此时MOS管DS未打通,ID=0;
2, 此时VGS增加,VGD会减小;
3, 第一阶段驱动对Ciss充电,主要是对CGS充电;
——若D与G完全没有回流通路,则不会对CGD放电,D极电压被抬升;事实上如果对于缓启动电路,D极有大电容接至GND,那相当于有一条间接的回流通路从G->D->S。

2. t1->t2:VGS达到MOS管开启电压,进入线性区,ID缓慢上升,至t2时刻ID到达饱和或是负载最大电流;
1, 本阶段VGS>VGS(th),此时MOS管DS已经打通,ID>0,且随VGS增加ID不断增大;
2, 此时由于D与S之间已导通,G与D之间的回流通路通过ID建立了起来,形成CGD的放电回路,对CGD进行放电;同时,继续对CGS充电;
3, 如下右图所示,t1->t2红色箭头的高度,取决于负载对ID电流大小的需求,并非是一个固定值;假如ID在VGS=5V即可满足负载对电流的需求,那么t1->t2阶段就将在VGS=5V结束;
4, 如下右图所示,在此阶段VDS一直承受近乎全部电压VDD,所以损耗较大。

3. t2->t3(米勒平台):t2时刻 ID达到饱和并维持稳定值,MOS管工作在饱和区;
1, 本阶段从ID电流角度来看,VGS电压已将MOS管完全打通,ID保持不变,VGS保持不变, 同时VDS电压开始下降;
2, 此阶段VGD先减小(VD>VG阶段)后反向增大(VG>VD阶段),对于CGD来说先放电后充电,对于CGS则不再消耗电荷(具体原理,下节“米勒平台”详细分析);
3, 米勒平台阶段ID电流很大,在平台期间MOS管损耗较大,同时它延长了MOS管的开关时间,对于快速开关的应用,要尽量减少米勒平台时间。

4. t3->t4:VDS电压下降到0V,VDD继续给CGS充电,直至VGS = VDD,MOS管完成导通过程;
1, 本阶段MOS管进入可变电阻区,随着VGS不断增加,RDS不断减小,ID值取决于负载的变化;
2, 此阶段VGS增加,VDS基本保持不变,VGD也随VGS同时增加,此时已结束米勒平台,所以CGD远小于CGS,VGS电压得以正常速度增大。

5. MOS管关断过程:是开通过程的反过程,如下图所示;
——关断过程与开启过程的步骤刚好相反,所以MOS管关断过程也同样存在较大的损耗。

3,米勒平台
我们已经知道了米勒平台是什么,它是MOS在开启或关断过程中, VGS电压维持不变的状态。那为什么会称它为米勒平台呢?是米勒老先生发现了MOS管上电过程中的这个“台阶”么?其实不然,米勒老先生发现的是:一种特殊运放电路结构导致反馈电容容值被放大的效应;人们称之为:米勒效应。而MOS管上的米勒平台正是由于米勒效应所产生的,米勒先生发现的这个效应听起来好像很悬,接下来,我们先从两个角度来了解米勒效应。
1. 第一种方法:如下图所示,我们假设一个增益为-Av的理想反向电压放大器(运放负极接输出),在放大器的输出和输入端之间跨接容抗为 Z = 1/(jωC)的电容,定义输入电流为 Ii,输入阻抗为 Zin;

1, 反向电压放大器增加了电路输入电容容值,并且放大系数为(1+Av):Zin = 1/[jωC*(1+Av)],计算过程如上图所示(如上式中复平面S=jω)。
2, 米勒发现的是:输入阻抗被缩小1/(1+Av)的这么一个效应;对于电容来说,容抗与容值成反比(容抗小,容值越大),所以相当于电容容值增加了(1+Av)倍。
2. 第一种方法是基于纯数学的推导,虽然数学推理肯定错不了,但还是感觉结论挺奇怪;是否有更加便于理解的方式呢?如下图所示,我们将反馈路径上的电容C0人为地分成C1和C2,并且C1和C2中间接到GND;
——C1 = C2 = C0,只是从充电电量(Q)的角度进行划分。

1, C1跨接在Vi和GND之间,那么电容C1两端的电压是:Vi;那么从充电电量(Q)的角度来看:C1 = C0;
2, C2跨接在GND和Vo之间,而Vo = -Av*Vi,所以电容C2两端的电压是:Av*Vi;所以从充电电量(Q)角度来看:C2 = Av*C0;
3, 所以C1和C2的充电电量加在一起:(1+Av)*C0,相当于电容C0的容量增加了(1+Av)倍。
——我们再来直观理解一遍:如果电源电压Vi直接加在C0上(C0两端电压为Vi),则其表现为C0电容值;但由于运放的作用,加在C0两端的电压变成(1+Av)*Vi,那么相同电容值的电量(Q)增加了(1+Av)倍,所以表现出来电容值被放大了(1+Av)倍。
这个效应最早是由 John Milton Miller 发现的并发表在他 1920的著作中,所以称之为米勒效应。米勒效应是跟运放相关,也还没扯到MOS管哪,跟米勒平台有什么关系呢?
如下图所示为MOS管的共源电路(common source):D为输出端,S接地,G为输入端;
1. 根据 MOS的小信号模型(具体可参考“半导体物理”相关书籍中的MOS管小信号分析章节), 形成一个反向电压放大器,其等效电路可以由右下图来表示;
2. CGD是跨接在输入(G)和输出(D)上的反馈电容,不同MOS管放大系数不同,最大可达几百倍。
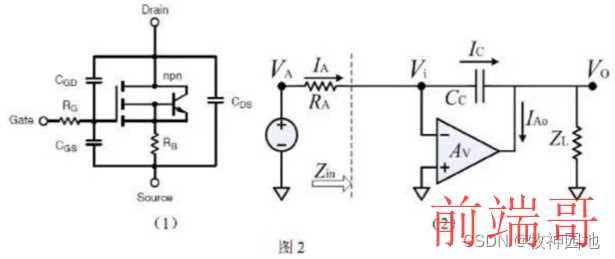
MOS管的开启过程就是MOS共源电路工作模式,此时CGD将会被放大n倍,变成米勒电容。正常情况下CGS比CGD要大很多,但一旦进入米勒平台时CGD反而远大于CGS了。
如下图所示,为什么CGD很大,CGS小就会导致VGS保持不变呢?
我们看到大多解释:在米勒平台阶段CGS相比CGS大很多,导致同时对CGS和CGD充电时,绝大多数电流通过CGS->D端->S端这条路径,而CGS只有非常小的电流流过,所以VGS基本保持不变。对于这个解释,我个人一直没有理解,所以也不认同。

那关于MOS管米勒平台,我是怎么理解的呢?首先我们假设负载电流在米勒平台阶段需求电流保持不变,分如下几个步骤来分析:
1. 首先,MOS管在米勒平台阶段,输入VGS和输出电压VDS是一个负反馈系统(输入VGS和输出电流ID是一个正反馈系统);
2. 其次,当VDS电压开始变小,MOS管进入米勒平台阶段,在这个电路中我们看到VS是GND不变的,所以是VD电压开始减小,一直到VDS为0时米勒平台结束;
3. 一旦VD减小,我们看到CGD两端的电压开始变小(接VD端电压大,VG端电压小),从VG的角度来看CGD开始充电,所以G端的驱动电流是有通道的;
4. 但是如何确定电流是全部流过CGD而不会流过CGS呢?
5. 我们可以看到:在VDS电压开始变化时,ID电流已经达到最大(根据负载需求,不取决于MOS管本身);
1, 如果VDS电压下降速度过快(不能维持VGS不变),VGS电压下降(下降速度超过电容电压充电速度),此时MOS管将会被稍微闭合一点,导致RDS增加,那么VDS电压下降速度会减缓,VGS电压会上升;
2, 如果VDS电压下降速度过慢,则必然会导致VGS电压上升(上升速度慢于电容电压充电速度),此时MOS管将会被打开大一点,导致RDS减小,那么VDS电压下降速度加快,VGS电压会下降;
3, 所以正常情况下VGS电压保持固定电平,由MOS管CGS寄生电容和负载电流的大小决定了VDS电压变化速度。
6. 那么如果VG电压突变,是否会导致米勒平台的混乱或变化呢?我们来看如下两个假设:
1, 假设VGS突然变大(RDS变小),此时VDS会突然变小(相对原VDS变化的速度);由于CGD电容两端的电压不能突变,VG电压就会变小;
2, 假设VGS突然变小(RDS变大),此时VDS会突然变大(相对原VDS变化的速度);由于CGD电容两端的电压不能突变,VG电压就会变大;所以MOS管的反馈机制会调整VGS的变化,就算外界干扰,也能自动调整回平衡状态。
所以从我个人对MOS管米勒平台分析来说:米勒平台本身就是由于MOS管开启/关闭阶段的负反馈机制所决定,而非因为米勒效应产生;但米勒效应将这个平台变长、变明显。明显到影响了MOS管的应用:
1. 影响MOS管的开关频率,开关损耗,要通过各种辅助手段极力减小它的影响;
2. 用于电源缓启动应用时,要通过辅助手段增加CGD来延长米勒平台。

